One distinguishing property of bosons versus fermions is the number of “rotations” required for the particle to return to the state in which it began. In other words, to achieve symmetry.
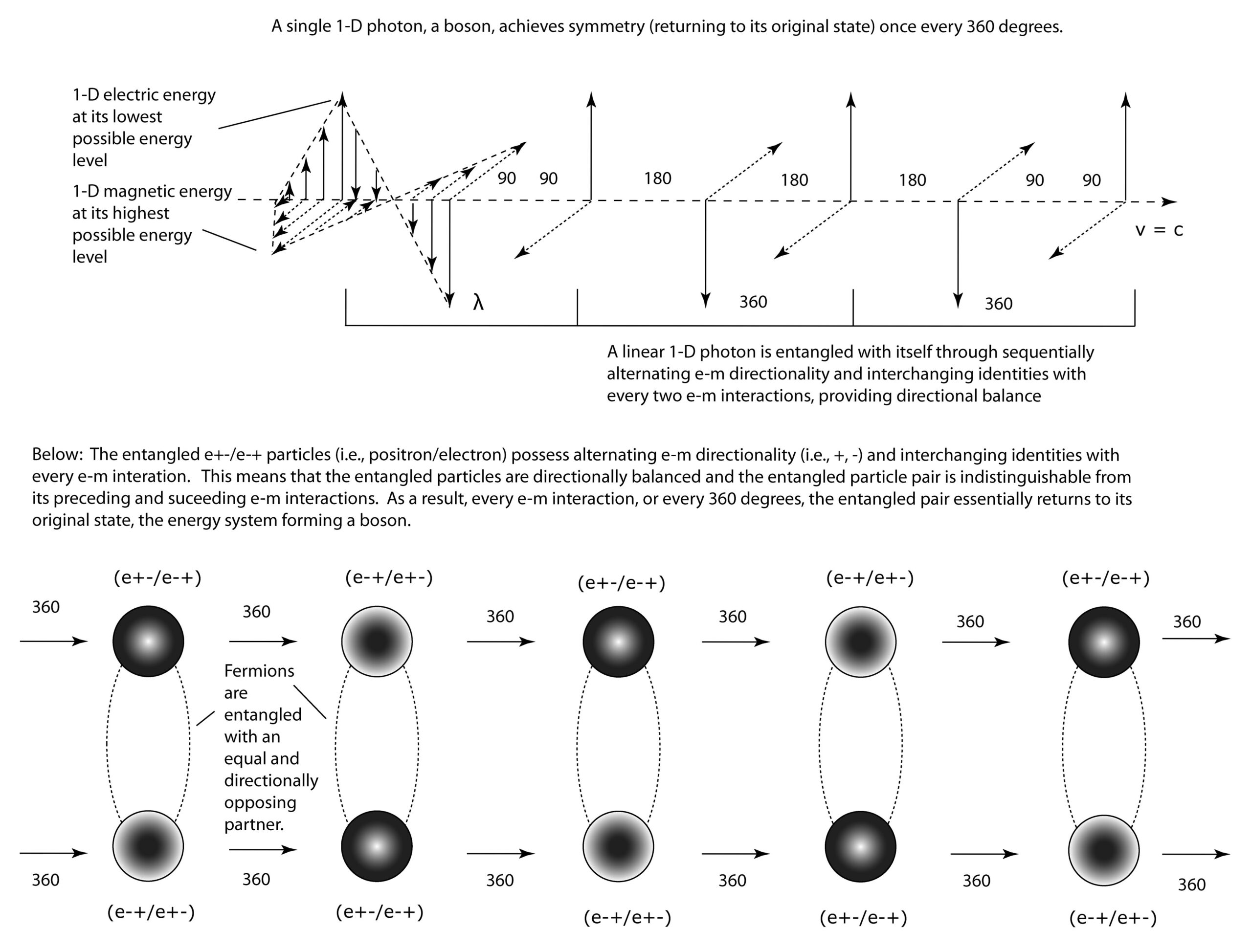
Bosons return to their original state, or achieve symmetry, once every 360 degrees. Fermions needs an extra “rotation” to return to their original state, or do so once every 720 degrees.
1-D electromagnetic photons are ‘authentic’ bosons due to being 1-dimensional (i.e., 1-D). While they alternate e-m directionality every 1/2 e-m interaction, or within a single e-m interaction or wavelength, they do not alternate e-m directionality from one e-m interaction to another. The 1-D photon ‘returns’ to its original state (i.e., symmetry) with every e-m interaction. Each 1-D e-m photon is sequentially entangled with itself once every two e-m interactions.
2-D electromagnetic particles consist of two possible opposing e-m directionalities, [-] and [+]. An e- particle, or electron, possesses 2-D electric energy diverging outward from system center toward a lower energy level (i.e., lower density). An e+ particle, or positron, possesses 2-D electric energy converging toward system center toward a higher energy level (i.e., higher density). When an electron and a positron are entangled, they each possess opposing alternating e-m directionality and interchanging identities with every e-m interaction. That is, each of the entangled e-+/e+- partners alternate between being an e- particle and being an e+ particle with every successive e-m interaction, so that the two particles are essentially ‘acting’ as opposing poles of a single energy entity, providing directional balance to each other with every e-m interaction.
Unlike unentangled e+ or e- particles, entangled (e+- and e-+) particles only possess the 2-D energy phase without 2-D magnetic energy required to provide directional balance (maybe?). Entangled particles provide each other with directional balance, allowing their energies to move in and out from system centers without having to recycle along their 1-D circumferences and back to or from system center along their axis of spin. They are in a wavefunction state in which the entangled partners alternate e-m directionality and interchange identities so that neither is distinguishable from the other. When they become disentangled, they revert back to going through both their 2-D phase (with energy flowing outward or inward relative to system center – one e-m interaction) and 1-D/2-D phase (in which their energies flow to or from their system centers – one e-m interaction), and are unidirectional (i.e., [-] or [+]) and are distinguishable from each other.
360 degrees vs. 720 degrees to return to original state
Entangled particle pairs also do not possess the phase with 1-D/2-D energy flowing along the circumference and to or from system center along the 1-D axis of spin. This is because each of the entangled partners simply exchange 2-D directionality with every e-m interaction (360 degree rotation), and as a result, provide each other with directional balance. So magnetic energy is not needed to provide directional balance. So entangled particles compose balanced energy systems that are bosons.
1-D electromagnetic photons, or ‘authentic’ (i.e., elementary) bosons, achieve symmetry with every e-m interaction or wavelength, or 360 degrees rotation, because they possess both possible e-m directionalities with every e-m interaction (i.e., the 1-D photon changes direction relative to system center (i.e., path of v = c) once every half e-m interaction).
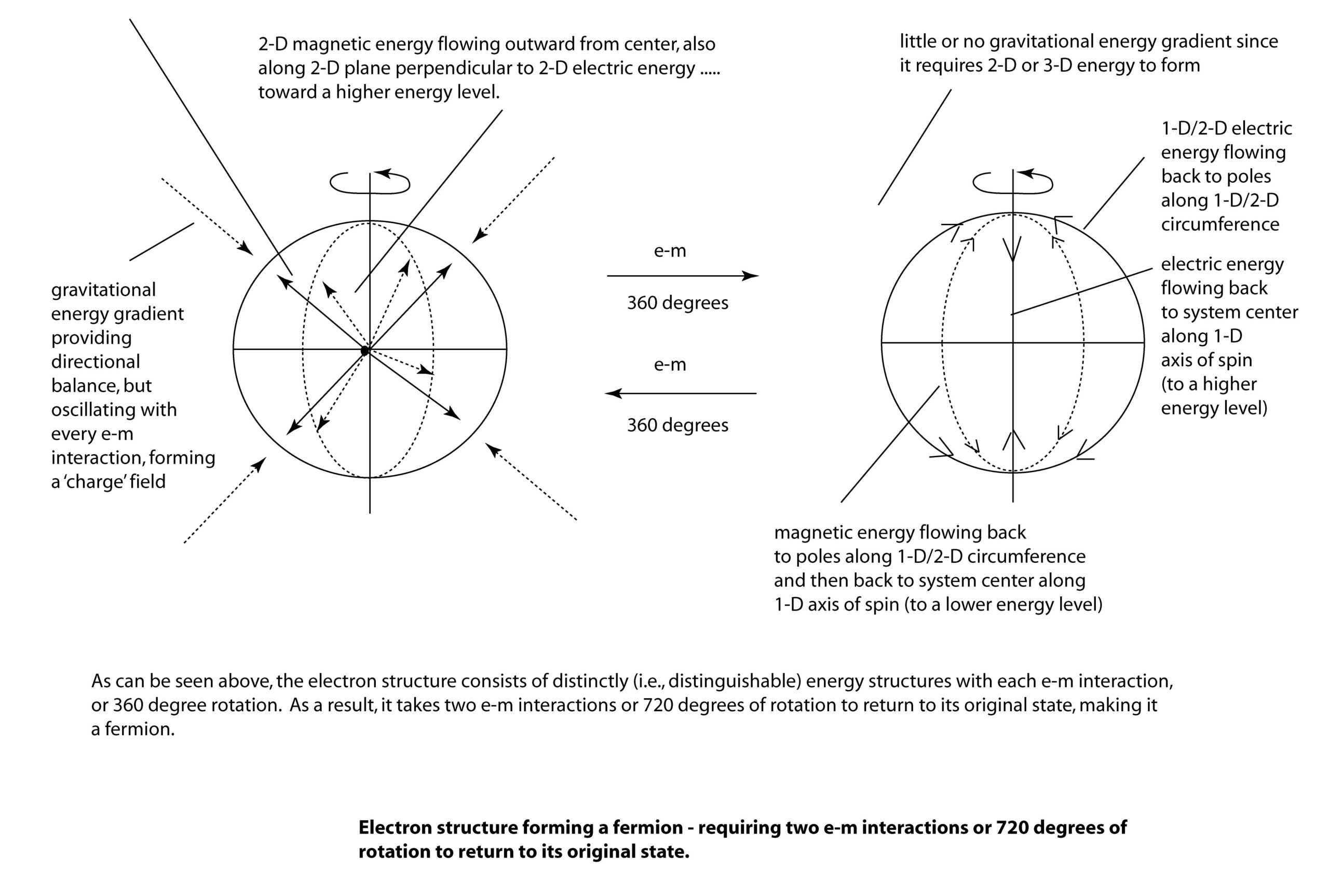
On the other hand, an unentangled 2-D particle (i.e., either an electron or a positron) consists of a 2-D energy phase in which the 2-D electric energy moves either outward from system center (i.e., electron) toward a lower energy level or inward to system center (i.e., positron) to a higher energy level. This represents one e-m interaction, or 360 degrees of rotation. The next e-m interaction consists of the electric energy flowing along the 1-D/2-D circumference to (i.e., for an electron) or from (i.e., for a positron) the particle’s poles, and to (i.e. electron) or from (i.e., positron) system center along the 1-D axis of spin. So in order for an entangled fermion to return to its original state, it takes two e-m interactions, or 720 degrees, to achieve symmetry.
Why does a non-entangled fermion take 720 degrees to achieve symmetry? It is probably due to the structure of a non-entangled 2-D e- or e+ particle. For instance, in the case of an electron (i.e., e- particle), its 2-D electromagnetic energy moves outward from system center in one e-m interaction, and then returns in the next e-m interaction along the 1-D axis of ‘spin’ to system center. So the 2-D/1-D electromagnetic energy will go through two e-m interactions – possibly equivalent to 720 degrees – before returning to its original state (i.e., achieving symmetry).
